斐波那契数列(Fibonacci sequence)
数列样板:0、1、1、2、3、5、8、13、21、34、……
定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)
特征:这个数列从第3项开始,每一项都等于前两项之和。
例子:兔子繁殖问题。兔子从出生到繁殖年龄的间隔时间为3个月,如果兔子没有死亡,每一对成年兔子每月可以繁育一对小兔,三个月之后小兔开始繁育,以此反复,求n月之后兔子的总对数。
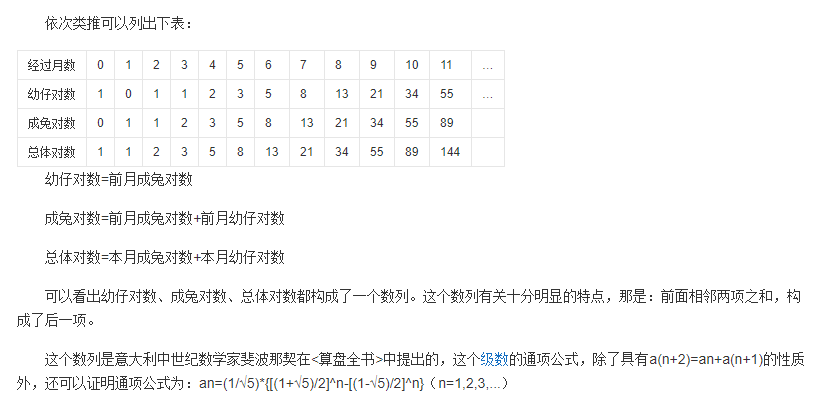
下图是百度百科的类推结果:
程序求解
递归方式:
int fibonacci(int n)
{
return (n < 3) ? 1 : fibonacci(n - 1) + fibonacci(n - 2);
}
这个代码看起来简单但是时间复杂度太高,O(2^n).
循环方式:
int feibonacii(int n)
{
int a=0,b=1,c=1,n;
for(int i=1;i<=n;i++)
{
a=b;
b=c;
c=a+b;
}
return c;
}
这个时间复杂度为O(n).
详解链接:斐波那契数列